Journées nationales du GDR GPL
Grenoble, 12-15 Juin 2018
Colocalisées avec AFADL, CAL et CIEL.

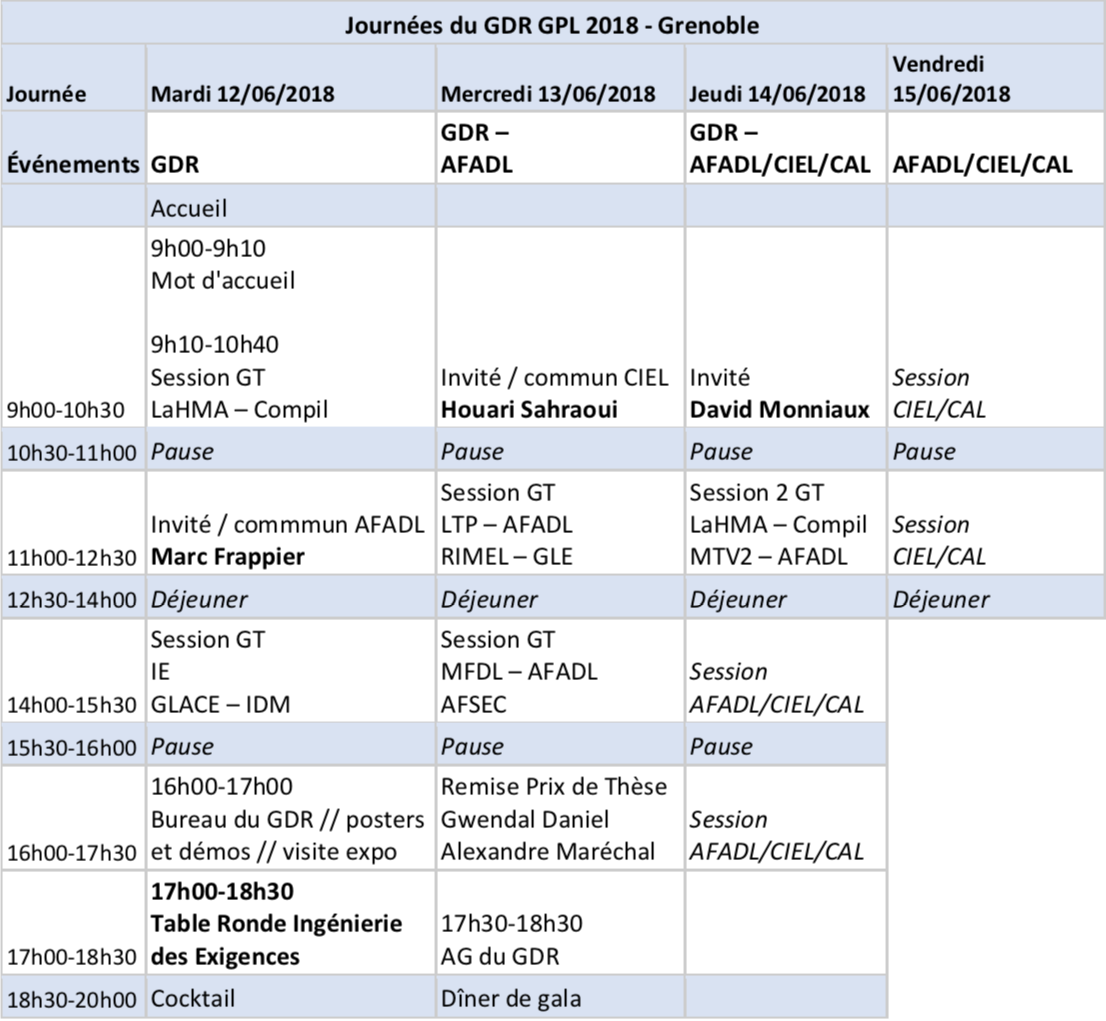
Programme détaillé : pdf

SMT-solving initiation

David Monniaux (Vérimag) David Monniaux est directeur de recherche au CNRS, au laboratoire VERIMAG, où il mène des recherches en vérification automatique de logiciels. Il travaille notamment sur l'algorithmique de la recherche d'invariants et de la preuve automatique; des travaux récents portent sur la recherche d'invariants sur les tableaux et autres structures de données, et sur le calcul efficace sur les polyèdres convexes. Par le passé, il a travaillé à l'analyse automatique de logiciels appliquée aux logiciels critiques, notamment avioniques, et fut des concepteurs et développeurs de l'outil Astrée. En 2012, il a été lauréat d'un financement ERC starting grant.

Résumé : Satisfiability modulo theory (SMT) consists in testing the satisfiability of first-order formulas over linear integer or real arithmetic, or other theories. In this survey, we explain the combination of propositional satisfiability and decision procedures for conjunctions known as DPLL(T), and the alternative "natural domain" approaches. We also cover quantifiers, Craig interpolants, polynomial arithmetic, and how SMT solvers are used in automated software analysis.

La visualisation des logiciels ou comment voir et explorer l’intangible

Houari Sahraoui est professeur de génie logiciel au département d’informatique et de RO de l’Université de Montréal, depuis 1999. Avant de rejoindre l'université, il a œuvré comme chercheur au Centre de Recherche en Informatique de Montréal. Il a obtenu un Doctorat en Informatique de l'Université Pierre et Marie Curie (1995), Paris, France, spécialisé en intelligence artificielle (méta-modélisation et transformation de modèles appliquées au génie logiciel). Ses intérêts de recherche portent sur le génie logiciel expérimental, les méthodes de recherche heuristique appliquées au génie logiciel, la visualisation, la transformation de modèles, ainsi que la réingénierie. Avec ses étudiants, il a publié près de 200 articles dans des revues, conférences et ateliers dont plusieurs ont reçu des prix. Il a été membre de comités de programme de nombreuses conférences internationales (IEEE et ACM), membre du comité de lecture de trois revues et organisateur de plusieurs conférences et ateliers. Il a été le président du comité de programme de VISSOFT 2011 et président de VISSOFT 2014.

Résumé : La visualisation des logiciels est un outil efficace et flexible pour effectuer des tâches de développement et de maintenance qui sont difficiles à automatiser. Elle permet l'exploration et l'analyse de grands ensembles de données multidimensionnelles extraites des logiciels. Durant les deux dernières décennies, de nombreux environnements de visualisation ont été proposés. Pour la plupart, ils utilisent des métaphores de visualisation intéressantes et sont capables de représenter des logiciels de grande taille. Cependant, on ne peut que constater qu’en général, leur utilisation est restreinte à la petite communauté qui les a développées. Ce phénomène s’explique par une adéquation discutable de ces environnements pour les tâches qu’ils sont censés supporter. En effet, les choix effectués lors du développement de ces environnements ne sont pas (explicitement) motivés par la nature des tâches ciblées. Il est donc difficile pour le commun des utilisateurs de les comprendre et d’apprendre à les utiliser dans des situations concrètes. Dans cet exposé, nous présentons les principes et les lignes directrices pour développer des outils de visualisation de logiciels en considérant explicitement la nature des données et des actions mises en œuvre dans les tâches de maintenance. Ces principes sont illustrés à travers l'environnement de visualisation VERSO.

Titre : Diagrammes états-transitions algébriques

Marc Frappier est professeur de génie logiciel au Département d’informatique de l’Université de Sherbrooke depuis 1996. Titulaire d’un doctorat en informatique de l’Université d’Ottawa (1995), ses intérêts de recherche portent sur la spécification, la synthèse et la construction de logiciels, la sécurité fonctionnelle, la gestion de projets ainsi que la mesure automatique de la taille fonctionnelle. Il a publié plus d’une soixantaine d’articles dans des revues et conférences internationales et est co-éditeur de deux livres. Avant de se joindre à l’Université de Sherbrooke, il a œuvré durant plus de 5 années en industrie à titre de consultant, analyste senior et gestionnaire de projets pour plusieurs entreprises. Ses activités industrielles l’ont amené à travailler dans divers domaines : manufacturier (Alcan et Cascades), bancaire (Banque royale du Canada, Banque Nationale du Canada, BFD/ÆBIS), pharmaceutique (Merck Frosst) aérospatial (Agence spatiale canadienne) et télécommunications (Nortel).

Résumé : Les diagrammes états-transitions algébriques (Algebraic State-Transition Diagrams - ASTD) sont une extension des Statecharts d'Harel en utilisant des opérateurs des algèbres de processus. Ces opérateurs permettent de composer des diagrammes d'états-transitions hiérarchiques. On retrouve la séquence, le choix, la fermeture de Kleene, la garde, la synchronisation et une version quantifiée du choix et de la synchronisation. Cette extension permet de conjuguer le pouvoir d'abstraction des algèbres de processus avec la représentation graphique des Statecharts. La construction itérative d'ASTD, par raffinement successif, sera présentée, en utilisant le raffinement d'état, de transition et de boucle. Deux mécanismes pour gérer les données d'un système seront présentés. Le premier permet un couplage avec le langage B, où chaque événement d'un ASTD est associé à une opération d'une machine B, qui encapsule les données. Dans le deuxième, on s'inspire de la tradition des Statecharts : des variables d'état sont déclarées dans les ASTD, et des actions sur les transitions et les états permettent de modifier ces variables d'état. Les outils permettant d'exécuter, de vérifier et de traduire en B les ASTD, ainsi que des algorithmes d'exécution efficace des ASTD, seront aussi présentés. Divers exemples d'application seront donnés : système d'information, système de contrôle de train, contrôle d'accès et détection d'intrusion en sécurité informatique.